Suatu gelombang berjalan merambat ke kiri pada tali yang sangat panjang dengan frekuensi 10 Hz dan cepat rambat gelombang 5 m/s. Jika amplitudo gelombang 10 cm dan arah getar pertama ke bawah, tentukan persamaan simpangan gelombang tersebut pada suatu titik yang berjarak x dari sumber gelombang!
Penyelesaian:
Diketahui : A = 10 cm = 0,1 m; f = 10 Hz dan v = 5 m/s
Ditanya: persamaan simpangan (y)
Jawab:
Arah getar pertama ke bawah : negatif (-)
Arah rambat ke kiri : positif (+)
Kecepatan sudut nya: ω = 2πf = 2π10 = 20π rad/s
Bilangan gelombang: k = 2π / λ
Mencari λ terlebih dahulu yaitu menggunakan persamaan: v = λ.f
λ = v/f
λ = 5/10 = 0,5 m
sehingga: k = 2π / λ
k = 2π / 0,5
k = 4π /m
Jadi persamaan simpangan gelombangnya adalah:
y = - A sin (ωt + kx)
y = - 0,1 sin (20πt + 4πx) atau y = - 0,1 sin π (20t + 4x)
==============================================
Perhatikan gambar berikut:
Jika periode gelombang 2 sekon, tentukan persamaan simpangan gelombang berjalan tersebut?
Pembahasan:
Berdasarkan gambar maka didapat:
Amplitudo (simpangan terjauh dari titik seimbang) A = 0,5 m
Panjang gelombang (panjang 1 gelombang) λ = 4 m
Periode (T) = 2 s, maka kecepatan sudutnya adalah:
maka ω = 2π/2 = π
Bilangan gelombangnya:
maka k = 2π / 4 = 0,5π /m
Dengan memasukan nilai A, ω dan k ke persamaan umum gelombang berjalan dengan arah rambat ke kanan dan arah getar pertama ke atas :
y = 0,5 sin (πt - 0,5πx) atau y = 0,5 sin π (t - 0,5x)
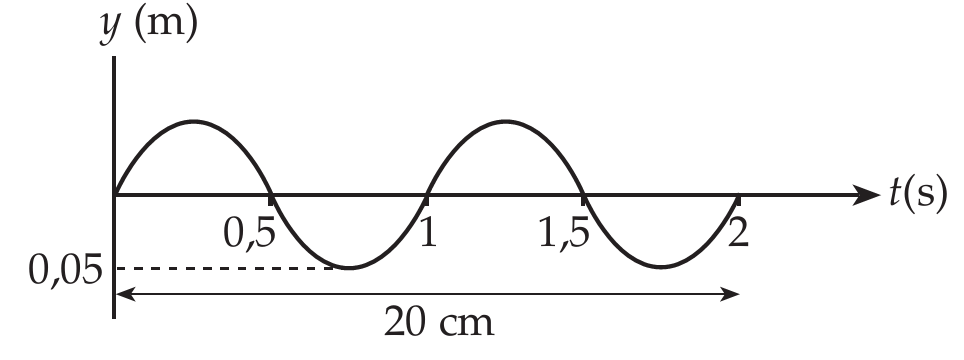
Perhatikan grafik y - t pada suatu gelombang berjalan berikut ini:
Tentukan persamaan simpangan gelombang pada grafik di atas!
Pembahasan:
Berdasarkan gambar maka didapat:
Amplitudo (simpangan terjauh dari titik seimbang) A = 5 cm = 0,05 m
Panjang gelombang (panjang 1 gelombang) 2λ = 1 m maka λ = 1/2 m = 0,5 m
Bilangan gelombang (k) adalah:
maka k = 2π/0,5 = 4π /m
Kecepatan sudutnya (ω) adalah:
Kita mencari dulu frekuensi (f). Frekuensi adalah banyaknya gelombang tiap sekon. Dari gambar diketahui banyaknya gelombang (n) = 2 gelombang dalam selang waktu (t) = 4 s maka frekuensinya adalah f = n/t = 2/4 = 0,5 Hz
Sehingga kecepatan sudutnya (ω) adalah: ω = 2πf = 2π0,5 = π rad/s
Dari perhitungan di atas kita dapatkan:
Arah getar pertama ke atas (+)
arah rambat ke kanan (-)
A = 0,05 m
ω = π rad/s
k = 4π
maka persamaaan simpangan gelombang berjalan grafik di atas adalah
y = 0,05 sin (πt - 4πx) atau y = 0,05 sin π(t - 4x)
================================================================
TUGAS
(Silakan jawabannya di tulis di kolom komentar)
Perhatikan grafik gelombang berjalan di bawah ini!





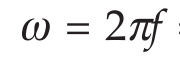


•diket: A= 0,05 m
BalasHapus^ (lamda)= 0,02/2= 0,01m
k (bil gel)= 2π/^ = 2π/0,01= 200π/m
•ditanya: persamaan gelombang
•dijawab:
kec.sud (w) adalah w= 2πf
~ f= n/t= 2/2= 1Hz
Jadi kecepatan sudutnya w = 2πf= 2π1=2π rad/s
*dari perhitungan di atas kita dapat,
-arah getar pertama ke atas (+)
-arah rambat ke kanan (-)
-A= 0,05 m
-w= 2π rad/s
-k= 200π
Maka persamaan gelombang berjalan grafik di atas adalah
y= 0,05 sin (2πt - 200πx)
dela sri lestari (Xl mipa 2)
Hapusoke mba dela
Hapusdela sri lestari (Xl mipa 2)
BalasHapusNama : AQSAH HILDA AL AUDI
BalasHapusKELAS:11MIPA 2
y = Asin(wt+kx)
w=2π/T
k =2π/£
£=20/2
=10cm
k=2π/10
T=2/2
=1s
w=2π/1
=2π
maka persamaan
y=0.05sin (2πt-2π/10x)
y=0.05sin 2π (t-1/10x)
itu persamaan y atas + , kok hasil dibawah persamaaan y nya -
Hapusdiket: A= 0,05 m
BalasHapus^ (lamda)= 0,02/2= 0,01m
k (bil gel)= 2π/^ = 2π/0,01= 100π/m
•ditanya: persamaan gelombang
•dijawab:
kec.sud (w) adalah w= 2πf
~ f= n/t= 2/2= 1Hz
Jadi kecepatan sudutnya w = 2πf= 2π1=2π rad/s
*dari perhitungan di atas kita dapat,
-arah getar pertama ke atas (+)
-arah rambat ke kanan (-)
-A= 0,05 m
-w= 2π rad/s
-k= 100π
Maka persamaan gelombang berjalan grafik di atas adalah
y= 0,05 sin (2πt - 100πx)
•diket: A= 0,05 m
BalasHapusλ= 0,02/2= 0,01m
k= 2π/^ = 2π/0,01= 200π/m
•ditanya: persamaan gelombang
•dijawab
w= 2πf
~ f= n/t= 2/2= 1Hz
Jadi kecepatan sudutnya w = 2πf= 2π1=2π rad/s
dari perhitungan di atas kita dapat:
-arah getar pertama ke atas (+)
-arah rambat ke kanan (-)
-A= 0,05 m
-w= 2π rad/s
-k= 200π
Maka persamaan gelombang berjalanadalah
y= 0,05 sin (2πt - 200πx)
Nur Muhammad
MIPA 2 \ 16