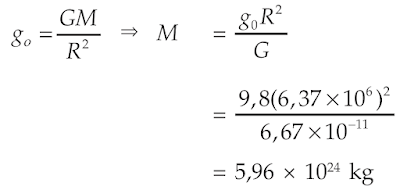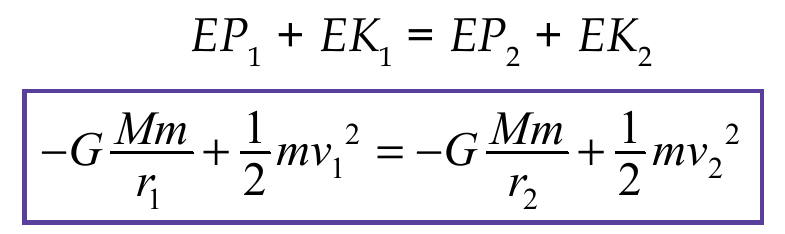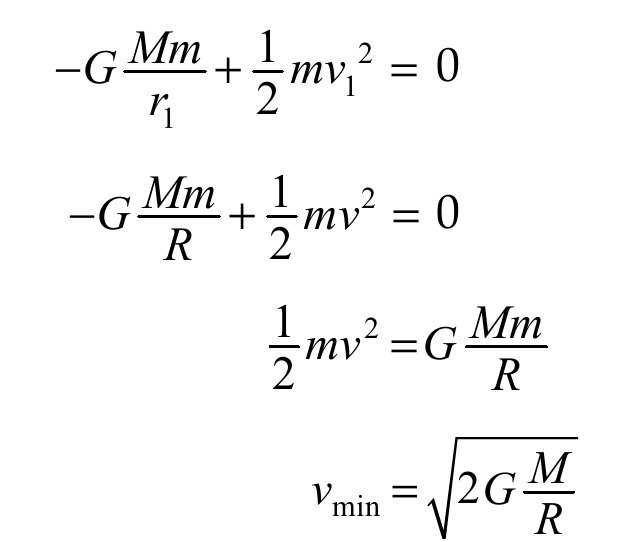بِسْــــــــــــــــمِ اﷲِالرَّØْÙ…َÙ†ِ اارَّØِيم
 |
| Sumber: news.detik.com |
Sebelum hukum gravitasi ditemukan oleh Newton, data-data tentang gerakan bulan dan planet-planet telah banyak dikumpulkan oleh para ilmuwan. Berdasarkan hukum gravitasi Newton, data-data tersebut digunakan untuk menghitung besaran lain tentang benda ruang angkasa yang tidak mungkin diukur dalam laboratorium.
Menghitung Massa Bumi
Massa bumi dapat dihitung dengan menggunakan nilai G yang telah diperoleh dari percobaan Cavendish. Anggap massa bumi Mdan jari-jari bumi R= 6,37 × 106 m (bumi dianggap bulat sempurna). Berdasarkan persamaan percepatan gravitasi bumi, Anda bisa menghitung besarnya massa bumi.
Menghitung Massa Matahari
Telah Anda ketahui bahwa jari-jari rata-rata orbit bumi rB = 1,5 × 1011 m dan periode bumi dalam mengelilingi matahari TB = 1 tahun = 3 × 107 s.
Berdasarkan kedua hal tersebut serta dengan menyamakan gaya matahari dan gaya sentripetal bumi, maka dapat diperkirakan massa matahari.
Menghitung Kecepatan Satelit
Anggap suatu satelit bermassa mbergerak melingkar mengelilingi bumi pada ketinggian hdari permukaan bumi. Massa bumi Mdan jari-jari bumi R. Anda tinjau gerakan satelit dari pengamat di bumi. Di sini gaya yang bekerja pada satelit adalah gaya gravitasi. Berdasarkan Hukum II Newton, kita bisa menghitung kecepatan satelit sebagai berikut:
Menghitung Jarak Orbit Satelit Bumi
Apabila satelit berada pada jarak rdari pusat bumi, maka kelajuan satelit saat mengorbit bumi dapat dihitung dengan menyamakan gaya gravitasi satelit dan gaya sentripetalnya.
Untuk posisi orbit geosinkron, yaitu bila periode orbit satelit sama dengan periode rotasi bumi, maka jari-jari orbit satelit dapat ditentukan sebagai berikut:
Menentukan Kecepatan Lepas dari Bumi
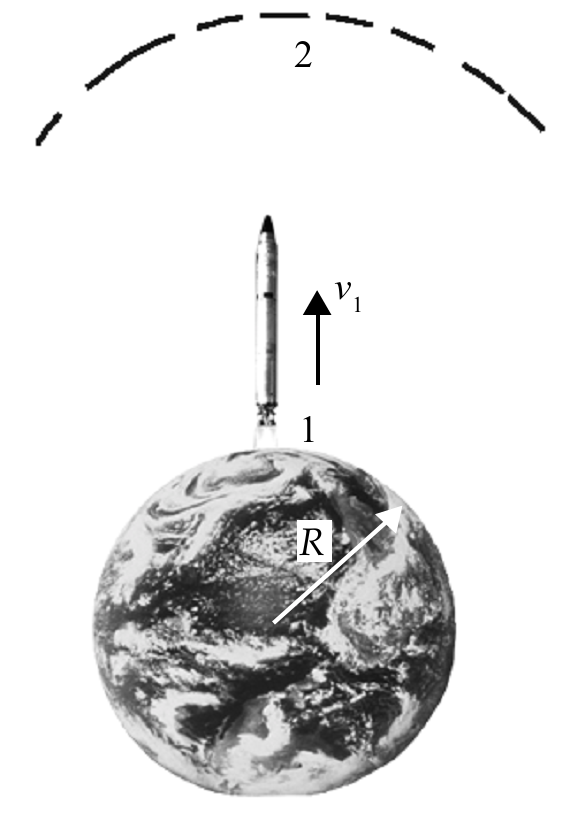
Apakah mungkin sebuah benda yang digerakkan atau ditembakkan vertikal ke atas tidak kembali ke Bumi? Jika mungkin terjadi, berapa kecepatan minimum benda tersebut saat di tembakkan agar terlepas dari pengaruh gravitasi Bumi? Untuk menjawab pertanyaan tersebut, perhatikanlah gambar sebuah roket yang sedang lepas landas pada Gambar berikut:
Kecepatan lepas adalah kecepatan minimum suatu benda agar saat benda tersebut dilemparkan ke atas tidak dapat kembali lagi. Kecepatan lepas sangat dibutuhkan untuk menempatkan satelit buatan pada orbitnya atau pesawat ruang angkasa. Besarnya kecepatan lepas yang diperlukan oleh suatu benda sangat erat kaitannya dengan energi potensial gravitasi yang dialami oleh benda tersebut.
Jika resultan gaya luar yang bekerja pada benda sama dengan nol, energi mekanik benda kekal. Secara matematis, Hukum Kekekalan Energi Mekanik memenuhi persamaan:
Agar roket lepas dari pengaruh gravitasi Bumi maka EP2 = 0, sedangkan kecepatan minimum roket diperoleh jika EK2 = 0. Dengan demikian, akan dihasilkan persamaan:
Karena g = GM/R2 maka diperoleh persamaan kecepatan minimum roket agar dapat lepas dari gravitasi Bumi sebagai berikut:
